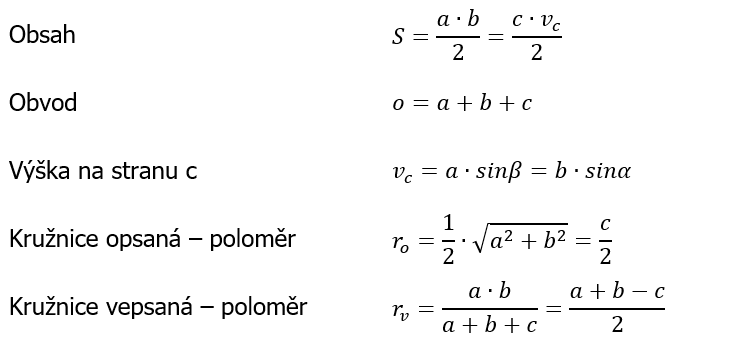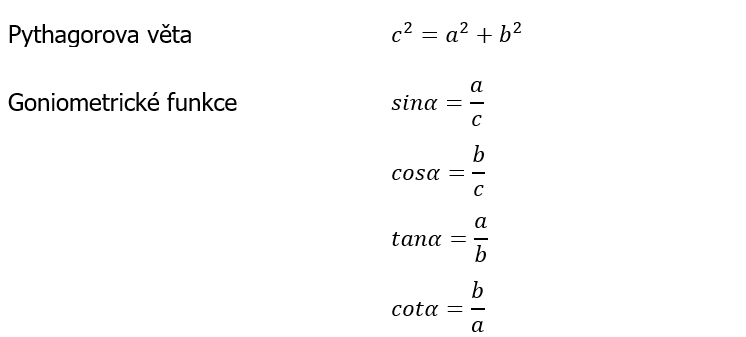Pravoúhlý trojúhelník
Výpočet
Do bílých polí zadejte vstupní hodnoty.
V šedých polích se automaticky zobrazí výsledky.
| Zvolte jednotku | |||
| odvěsna | |||
| a | = | ||
| odvěsna | |||
| b | = | ||
| přepona | |||
| c | = | ||
| obsah | |||
| S | = | ||
| obvod | |||
| o | = | ||
| výška na stranu c | |||
| vc | = | ||
| kružnice opsaná - poloměr | |||
| ro | = | ||
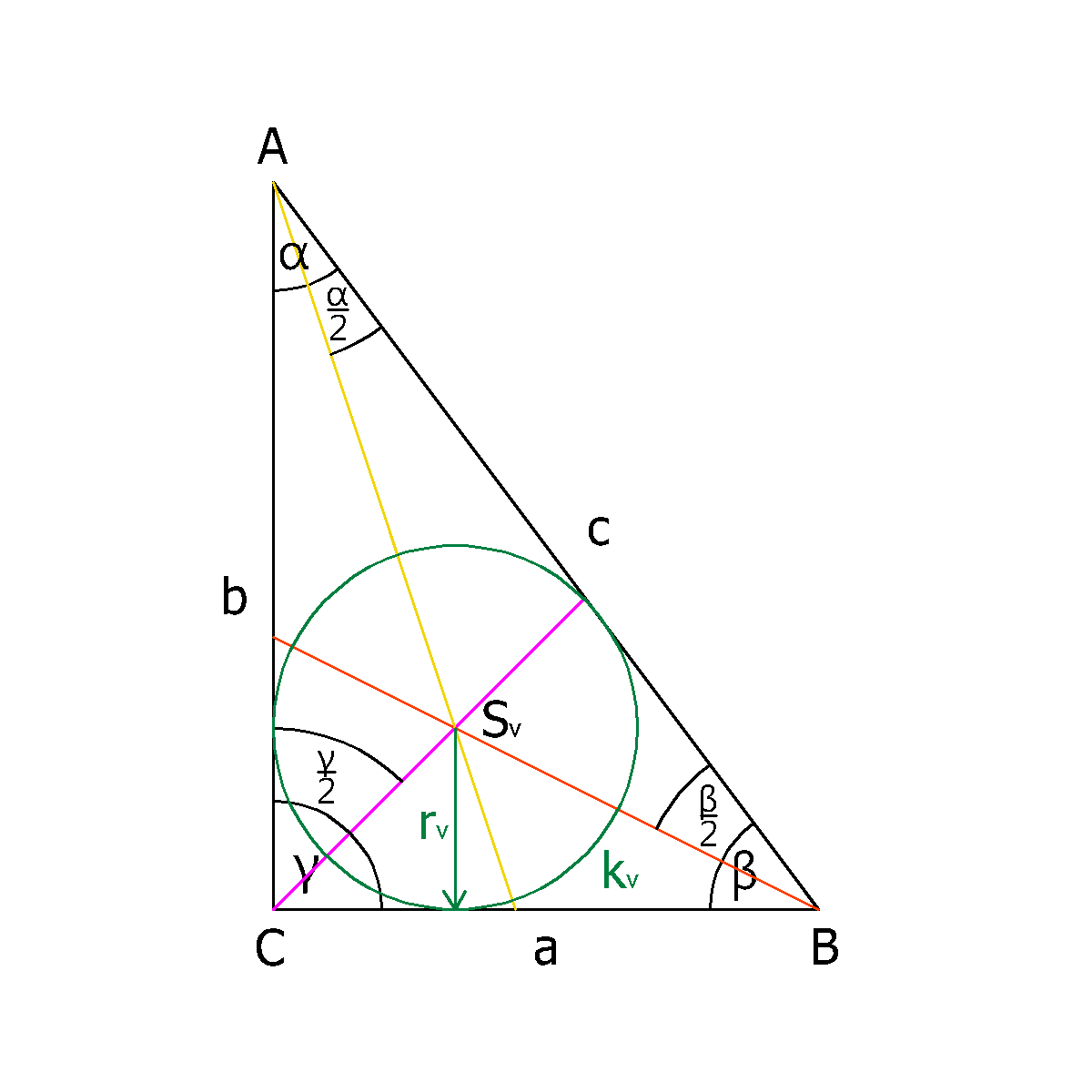
| kružnice vepsaná - poloměr | |||
| rv | = | ||
| úhel | |||
| α | = | ||
| úhel | |||
| β | = | ||
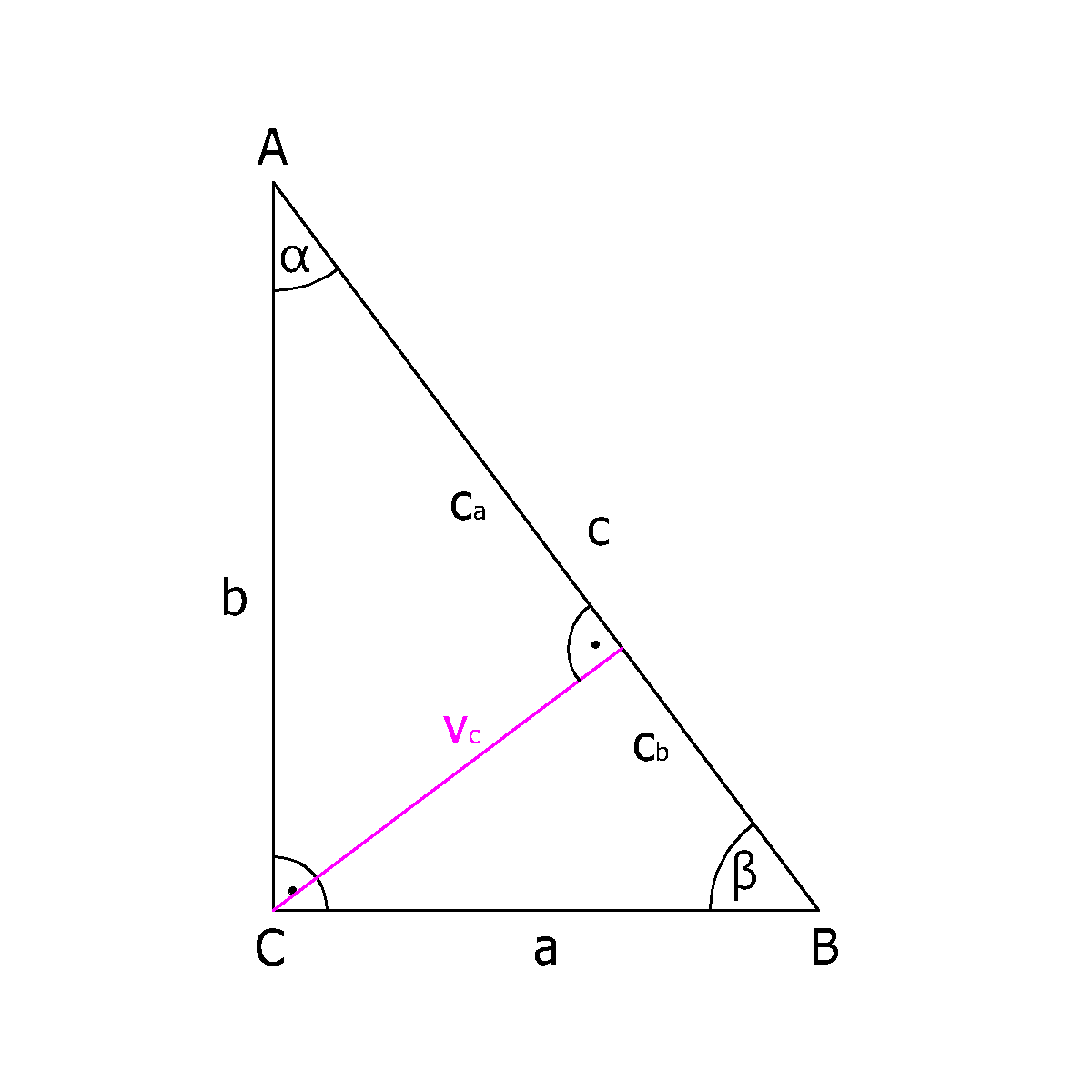
Pravoúhlý trojúhelník je takový trojúhelník, jehož jeden vnitřní úhel je pravý (90°) → dvě ze stran pravoúhlého trojúhelníka jsou na sebe kolmé.
Nejdelší strana pravoúhlého trojúhelníka, protilehlá pravému úhlu, je přepona. Zbylé dvě strany se označují jako odvěsny.
 |
 |
 |
 |
Základní vlastnosti:
- Mezi délkami stran pravoúhlého trojúhelníka platí Pythagorova věta
- Pro pravoúhlý trojúhelník platí Euklidovy věty
- Pravoúhlý trojúhelník je základem pro definici goniometrických funkcí
- Součet vnitřních úhlů trojúhelníku je 180° (α+β = 90° a ϒ = 90°)
- Velikost těžnice tc v pravoúhlém trojúhelníku je rovna poloměru opsané kružnice ro.
Pythagorova věta
c2 = a2 + b2
Obsah čtverce sestrojeného nad přeponou libovolného pravoúhlého trojúhelníku je roven součtu obsahů čtverců nad oběma jeho odvěsnami.
Euklidova věta o výšce
vc2 = ca · cb
Obsah čtverce sestrojeného nad výškou pravoúhlého trojúhelníka je roven obsahu obdélníka sestrojeného z obou úseků přepony.
Euklidova věta o odvěsně
a2 = c · ca
b2 = c · cb
Obsah čtverce sestrojeného nad odvěsnou pravoúhlého trojúhelníku je roven obsahu obdélníku sestrojeného z přepony a úseku přepony k této odvěsně přilehlé.